Have you ever felt overwhelmed by the large number of features when approaching a machine learning task?
Most data scientists experience this overwhelming challenge daily. While adding features enriches the data, it often slows down the training process and makes detecting hidden patterns more difficult, leading to the famous curse of dimensionality (in) .
Moreover, in high-dimensional space, surprising phenomena occur. To describe this concept with an analogy, think of the novel Flatland, where characters living in a flat (2-dimensional) world find themselves astonished when they encounter a 3-dimensional being. In a similar way, we struggle to understand that, in high-dimensional space, most points are exceptions and the distance between points is often greater than expected. All these phenomena, if not handled properly, can have dire consequences for our machine learning models.
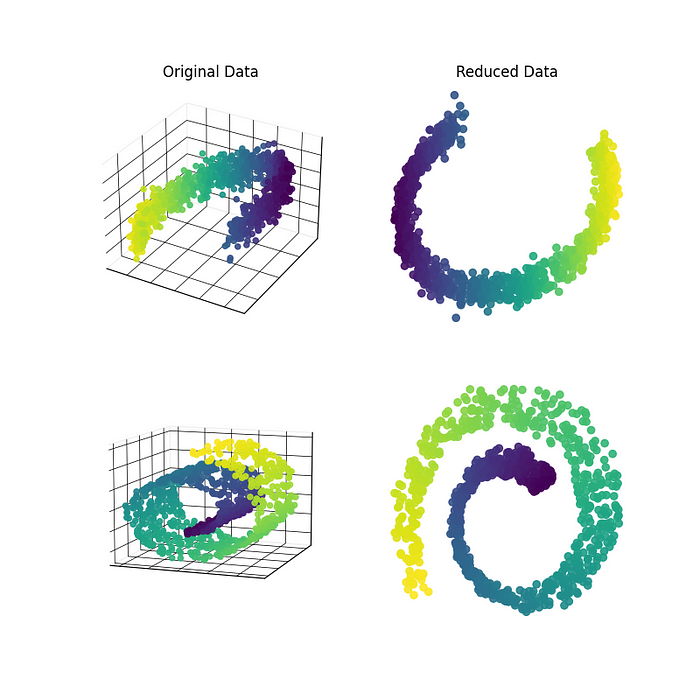
In this post, I will explain some advanced dimensionality reduction techniques used to mitigate this issue.
In my previous article, I introduced the relevance of dimensionality reduction in machine learning problems and how to overcome the curse of dimensionality, and I explained both the theory and implementation in Scikit-learn of the principal component analysis algorithm.
Following this, I will delve into additional dimensionality reduction algorithms, such as KPCA or LLE, which address the limitations of PCA.
Don't worry if you haven't read my Introduction to Dimensionality Reduction. This post is a standalone guide as I will detail each concept in simple terms. However, if you want to know more about PCA, I actively recommend this guide to serve your purpose:
